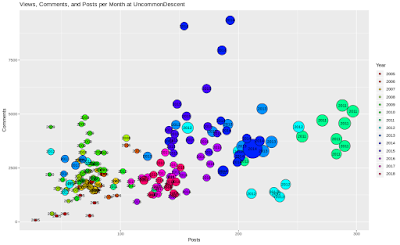
 Here are the posts and comments which Uncommon Descent received for each month from Apr 2005 until Dec 2018. The area of the circles is proportional to the number of views those posts gathered until mid-February 2019 (and most probably starting sometimes in 2011...)
Here are the posts and comments which Uncommon Descent received for each month from Apr 2005 until Dec 2018. The area of the circles is proportional to the number of views those posts gathered until mid-February 2019 (and most probably starting sometimes in 2011...)
Wednesday, February 27, 2019
Posts at Uncommon Descent
 Here are the posts and comments which Uncommon Descent received for each month from Apr 2005 until Dec 2018. The area of the circles is proportional to the number of views those posts gathered until mid-February 2019 (and most probably starting sometimes in 2011...)
Here are the posts and comments which Uncommon Descent received for each month from Apr 2005 until Dec 2018. The area of the circles is proportional to the number of views those posts gathered until mid-February 2019 (and most probably starting sometimes in 2011...)
Friday, February 23, 2018
An Amazon Review: Still waiting for the ultimate book on Intelligent Design
We are all waiting for the ultimate book on Intelligent Design, written by R. Marks and W. Dembski. Instead we get a "textbook", another attempt to explain the concepts to laymen. I got the impression that the authors used this setting to avoid the necessary rigour: they just do not define terms like "search" which they use hundreds of times. This allows for a lot of hand-waving, like the following sentence on p. 174:Not surprisingly, I gave it only two stars.
"We note, however, the choice of an algorithm along with its parameters and initialization imposes a probability distribution over the search space"
That unsubstantiated claim is essential for their following proofs on "The Search for a Search"!
And then there are details like this one:
p. 130: "For the Cracker Barrel puzzle [we got] an endogenous information of I = 7.15 bits"
p. 138: "We return now to the Cracker Barrel puzzle. We showed that the endogenous information [...] is I = 7.4 bits"
I tried to solve this conundrum, but I came up with I = 7.8 bits. I contacted the authors, but got no reply.
Some Details on the Cracker Barrel Puzzle
A more complete quote from p. 130 is:For the Cracker Barrel puzzle, all of the 15 holes are filled with pegs and, at random, a single peg is removed. This starts the game. Using random initialization and random moves, simulation of four million games using a computer program resulted in an estimated win probability p = $0.007\,0$ and an endogenous information of $$I_\Omega = − \log_2\,p\;=\;7.15\,bits.$$They didn't calculate the correct value, but they simulated the puzzle 4,000,000. A simulation is the most easy programmable way to get a result - but how good is it? It should be pretty good: performing one simulation is a Bernoulli trial with a probability of success $p_t$, the theoretical probability to win a single game by chance. Repeating 4,000,000 Bernoulli trials leads to a binomial experiment $B(4,000,000; p_t)$, so $\sigma = 0.000\,042$ for $p_t$ - that's why stating four positions after the decimal point isn't overconfident: assuming that there is no systemic error, then the probability that the actual value $p_t$ lies within $0.007\,00 \pm 0.000\,05$ is $77\%$.
Giving three significant digits for $I_\Omega$ oversells the power of their experiment slightly: this implies that they expect $p_t$ to be in the interval $[0.007\,067;0.007\,065]$ with a reasonable probability - but the probability is at best about $44\%$.
Confining themselves to only two significant digits on p. 138: $I_\Omega = 7.4\;bits$ yields much more reliable results: again, assuming that there is nothing systematically wrong with their calculation, they can say that $p_t$ is in $[0.005\,72;0.006\,30]$ with a probability of more than $99.999\,99\%$! Well done...
Or not: it is very improbably that both values are correct. Very, very, very, very - using the most favourite estimations, then the second result should only occur with a probability of less than $10^{-98}$ if the first experiment was correctly implemented. It is even worse the other way around: $10^{-112}$.
Which value is correct?
Not surprising the answer: both are wrong - the three authors somehow botched the implementation of even the easiest way to approach the question - a simulation. How can I be so cock-sure? I simulated it myself - 4,000,000 times - and got a value of $p = 0.004\,5$. Then, I calculated the theoretical value by enumerating all possible games and their respective probabilities: again, $p = 0.004\,5$. Then, I published part of my code at The Sceptical Zone, and thankfully, Roy and Corneel also implemented a simulation - which got compatible results. Lastly, Tom English programmed the problem much more cleverly, getting exactly the same results as I (I just had to wait for mine much longer...)
Why didn't the authors do the same?
Monday, January 29, 2018
The Search Problem of William Dembski, Winston Ewert, and Robert Marks
Subjects: Evolutionary computation. Information technology–Mathematics.1
Thursday, January 18, 2018
Prof. Marks gets lucky at Cracker Barrel
Subjects: Evolutionary computation. Information technology–Mathematics.1
A search typically requires initialization. For the Cracker Barrel puzzle, all of the 15 holes are filled with pegs and, at random, a single peg is removed. This starts the game. Using random initialization and random moves, simulation of four million games using a computer program resulted in an estimated win probability p = 0.0070 and an endogenous information of $$I_\Omega = -\log_2 p = 7.15 bits.$$ Winning the puzzle using random moves with a randomly chosen initialization (the choice of the empty hole at the start of the game) is thus a bit more difficult than flipping a coin seven times and getting seven heads in a rowNaturally, I created such an simulation in R for myself: I encoded all thirty-six moves that could occur in a matrix
cb.moves, each row indicating the jumping peck, the peck which is jumped over, and the place on which the peck lands.
And here is the little function which simulates a single random game:
cb.simul <- function(pos){
# pos: boolean vector of length 15 indating position of pecks
# a move is allowed if there is a peck at the start position & on the field which is
# jumped over, but not at the final position
allowed.moves <- pos[cb.moves[,1]] & pos[cb.moves[,2]] & (!pos[cb.moves[,3]])
# if now move is allowed, return number of pecks left
if(sum(allowed.moves)==0) return(sum(pos))
# otherwise, chose an allowed move at random
number.of.move <- ((1:36)[allowed.moves])[sample(1:sum(allowed.moves),1)]
pos[cb.moves[number.of.move,]] <- c(FALSE,FALSE,TRUE)
return(cb.simul(pos))
}
cb.eval <-
function(pos, prob){
#pos: boolean vector of length 15 indicating position of pecks
#prob: the probability with which this state occurs
# a move is allowed if there is a peck at the start position & on the field which is
#jumped over, but not at the final position
allowed.moves <- pos[cb.moves[,1]] & pos[cb.moves[,2]] & (!pos[cb.moves[,3]])
if(sum(allowed.moves)==0){
#end of a game: prob now holds the probability that this game is played
nr.of.pecks <- sum(pos)
#number of remaining pecks
cb.number[nr.of.pecks] <<- cb.number[nr.of.pecks]+1
#the number of remaining pecks is stored in a global variable
cb.prob[nr.of.pecks] <<- cb.prob[nr.of.pecks] + prob
#the probability of this game is added to the appropriate place of the global variable
return()
}
for(k in 1:sum(allowed.moves)){
#moves are still possible, for each move the next stage will be calculated
d <- pos
number.of.move <- ((1:36)[allowed.moves])[k]
d[cb.moves[number.of.move,]] <- c(FALSE,FALSE,TRUE)
cb.eval(d,prob/sum(allowed.moves))
}
}
An educated guess
I found it odd that the authors run 4,000,000 simulations - 1.000,000 or 10,000,000 seem to be more commonly used numbers. But when you look at the puzzle, you see that it was not necessary for me to look at all fifteen possible starting positions - whether the first peck is missing in position 1 or position 11 does not change the quality of the game: you could rotate the board and perform the same moves. Using symmetries, you find that there are only four essentially different starting positions. the black, red, and blue group with three positions each, and the green group with six positions. For each group, you get a different probability of success| group | black | green | red | blue | prob. of choosing this group | .2 | .4 | .2 | .2 | prob. of success | .00686 | .00343 | .00709 | .001726 |
Is it a big deal?
It is easily corrigible: instead of "For the Cracker Barrel puzzle, all of the 15 holes are filled with pegs and, at random, a single peg is removed." they could write "For the Cracker Barrel puzzle, all of the 15 holes are filled with pegs and, one peck at the tip of the triangle is removed." If the book was actually used as a textbook, the simulation of the Cracker Barrel puzzle is an obvious exercise. I doubt that it is used that way anywhere, so no pupils were annoyed. It is somewhat surprising that such an error occurs: it seems that the program was written by a single contributor and not checked. That seems to have been the case in previous publications, too. Perhaps the authors thought that the program was too simple to be worthy of the full attention - and the more complicated stuff is properly vetted. OTOH, it could be a pattern.... Well, it will certainly be changed in the next edition.Monday, January 8, 2018
Monday, July 17, 2017
A letter to Winston Ewert
Dear Winston,
congratulations for publishing your first book! It took me some time to get to read it (though I'm always interested in the output of the Evo Lab). Over the last couple of weeks I've discussed your oeuvre on various blogs. I assume that some of you are aware of the arguments at UncommonDescent and TheSkepticalZone, but as those are not peer reviewed papers, the debates may have been ignored. Fair to say, I'm not a great fan of your new book. I'd like to highlight my problems by looking into two paragraphs which irked me during the first reading: In your section about "Loaded Die and Proportional Betting", you write on page 77:
The performance of proportional betting is akin to that of a search algorithm. For proportional betting, you want to extract the maximum amount of money from the game in a single bet. In search, you wish to extract the maximum amount of information in a single query. The mathematics is identical"This is at odds with the previous paragraphs: proportional betting doesn't optimize a single bet, but a sequence of bets - as you have clearly stated before. I'm well aware of Cover's and Thomas's "Elements of Information Theory", but I fail to say how their chapter on "Gambling and Data Compression" is applicable to your idea of a search. I tried to come up with an example, but if I have to search two equally sized subsets $\Omega_1$ and $\Omega_2$, and the target is to be found in $\Omega_1$ with a probability bigger than to be found in $\Omega_2$, proportional betting isn't the optimal way to go! Does proportional betting really extract the maximum of information in a single guess? Then there is this following paragraph on page 173:
One’s first inclination is to use an S4S search space populated by different search algorithms such as particle swarm, conjugate gradient descent or Levenberg-Marquardt search. Every search algorithm, in turn, has parameters. Search would not only need to be performed among the algorithms, but within the algorithms over a range of different parameters and initializations. Performing an S4S using this approach looks to be intractable. We note, however, the choice of an algorithm along with its parameters and initialization imposes a probability distribution over the search space. Searching among these probability distributions is tractable and is the model we will use. Our S4S search space is therefore populated by a large number of probability distributions imposed on the search space.Identifying/representing/translating/imposing a search and a probability distribution is central to your theory. It's quite disappointing that you are glossing over it in your new book! While you give generally a quite extensive bibliography, it is surprising that you do not quote any mechanism which translates the algorithm in a probability distribution. Therefore I do not know whether you are thinking about the mechanism as described in "Conservation of Information in Search: Measuring the Cost of Success": this one results in every exhaustive search finding its target. Or are you talking about the "representation" in "A General Theory of Information Cost Incurred by Successful Search": here, all exhaustive searches will do on average at best as a single guess (and yes, I think that this in counter-intuitive). As you are talking about $\Omega$ and not any augmented space, I suppose you have the latter in mind... But if two of your own "representations" result in such a difference between probabilities ($1$ versus $1/|\Omega|$), how can you be comfortable with making such a wide-reaching claim like "each search algorithm imposes a probability distribution over the search space" without further corroboration? Could you - for example - translate the damping parameters of the Levenberg-Marquardt search into such a probability distribution? I suppose that any attempt to do so would show a fundamental flaw in your model: the separation between the optimum of the function and the target.... I'd appreciate if you could address my concerns - at UD, TSZ, or my blog. Thanks,
Yours Di$\dots$ Eb$\dots$ P.S.: I have to add that I find the bibliographies quite annoying: why can't you add the number of the page if you are citing a book? Sometimes the terms which are accompanied by a footnote cannot be found at all in the given source! It is hard to imagine what the "humble authors" were thinking when they send their interested readers on such a futile search!
Tuesday, February 2, 2016
Some Pies for "The Skeptical Zone"

|

|
| In 2015, there some 45,000 comments were made at The Skeptical Zone. Here are the top ten of the commentators (just a quantitative, not a qualitative judgement.) I'll stick to the color scheme for all of figures in this post... | "The Skeptical Zone" has a handy "reply to"-feature, which allows you to address a previous comments (with or without inline quotation.) It is used to various degree - and though some don't use it at all, nearly 50% of all comments were replies. |





